- binary search
在一个已经排好序的数组上,O(logn )复杂度
先找mid=start+end。 array[mid]=val1,然后判断target,val1<target,就向右找,小于则向左找。重复上述过程, mid2=(end+mid)/2只取整数。
写一些函数的时候,先判断input是不是null或length==0?
某些情况下比如while(start+1<end)的话要单独判断end和start是不是target
为什么不是start<end退出,比如下面的例子,找最后一个出现的位置。【2,2】
while(start<end){
mid=(0+1)/2=0;
if (mid==target){ start =mid;}
}
应该用相邻或相等退出,即start+1<end;
求最后出现的位置: if找到了就向右找,
而且也要先判断end==target
第一个出现的位置,if找到了就向左找。
而且要先判断start==target。
而且mid= start+(end-start)/2 更不容易overflow,算是一个小的优化
模板:
while (start+1< end){
mid=start+(end-start)/2;
if(num[mid]==target) {return mid}
else if( >){ end=mid}
else{ start=mid }
if start==target
if end==target.
}
推荐写一些子 函数维持宏观框架
例题: find K closet elements
思路: 可以先bSearch找到target,然后双指针两边走
先看输出类型,新建好。
然后先写出思路, 然后把子程序的接口写出来,定义出来,input和output,然后写出来子函数的作用:output是什么
- Heap
大顶堆和小顶堆,min-heap和max-heap。
每一个node满足:father>=childs (max)
father<=childs(min)
左右没有关系
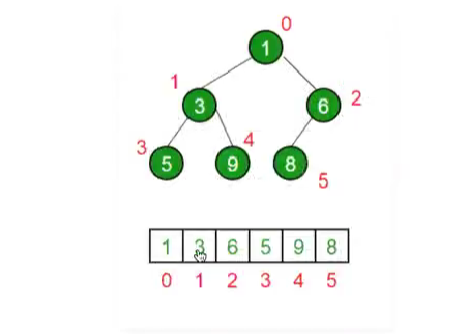
binary heap representation:
现在node为A【i】,
Arr[(i-1)/2] is the parent node.
Arr[2i+1] is the left child
Arr[2i+2] is the right child
复杂度:getMini() :对于Min-heap是一个O(1)
extractMin(): remove the root ,O(logn)
insert(): O(logn)
delete(): O(logn)
- 重点!!!!!
- top K的题右3solution
- sort O(nlogn) 不是很好
- quick select. (on avarge O(n)),有时候快有时候慢。要求是要进行该方法,必须已经拿到全部的数据,万一新来的data,只能重新来一遍
- Heap O(nlogk),只需要size 为k的heap, insert 每一次都是logk,然后比n次,现实生活中k远小于n。更适合Stream data,可以适用于新来的data,新来一个数是O(logk)
例题:Kth largest element要用min-heap,因为和root比较,小的就不用insert,大的菜肴insert进去,因为,heap里面村的是k个最大的,
步骤:先建立一个k size的heap,直接加进去,然后对比,如果大于,则pop root之后push(元素 )

